Probability density function(PDF)와 Cumulative distribution function(CDF)

1. PDF

'확률밀도함수(PDF)란 정규화(Normalize)된 연속변수에 대한 히스토그램이다.'

확률 밀도란 연속 확률 변수가 일정 구간에 포함될 확률을 확률밀도라고 한다. 이를 함수로 나타내는 PDF는 위의 성질을 만족해야한다.

Histogram란, 도수 분포의 상태를 기둥 모양의 그래프로 나타낸 것. 즉 각 데이터들의 갯수를 세어 본 것이다. 여러 예시가 있겠지만, 나는 사진을 좋아해서 위 사진을 참고하면, 포토샵에서 볼 수 있는 히스토그램이다. 이미지의 각 색상, 또는 밝기의 데이터의 범위는 0부터 255까지라고 하면 값이 0인 것, 1인 것, ... , 254인 것, 255인 것의 갯수를 세어서 막대 바 모양으로 그래프를 그린다.(정수만 생각해보자)

Normalize란, 다 더했을때 1이 되게 맞춰주는 것 이다. 사진의 해상도가 256x256이라면 각 바의 값을 픽셀 수만큼 나누어 주면 되겠다. 값이 200인 Red의 개수가 100개였다면, 100/65536가 될 것이고 각각의 바를 다 더하면 1이 된다.

이 PDF를 f(value)라고 명명하고, 픽셀의 값이 이산적인 경우(1,2,3, ... ,254,255)에는 이 사진의 어떤 픽셀의 Red값이 200일 확률은? 이라는 질문에  f(200)가 답이라고 할 수 있을 것이다(bar의 가로 길이가 1임). 이렇게 셀수 있고 유한한 변수의 경우에는 확률 질량 함수(probability mass function)이라고 부르며 아래를 만족해야한다..

① f(x)≥0, ② ∑f(x)＝1, ③ 

하지만, 데이터가 연속적이거나 레졸루션(δ)을 고려해야한다면 질문자체가 Red값이 200 + δ일 확률은? 이라고 물어야하고 그 의미를 포함하는 바의 면적을 확률로 답해야 할 것이다. 

2. CDF

'PDF를 누적하면 CDF(누적 분포함수)'

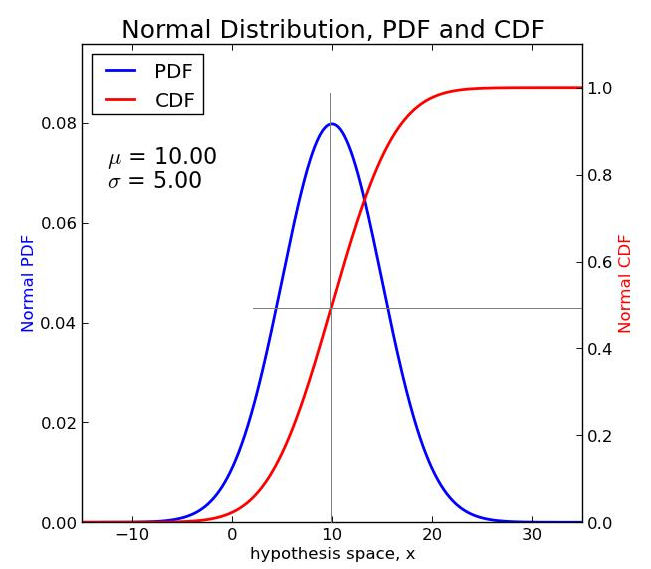
CDF는 PDF를 누적한 것이다. 즉 PDF를 적분하면 CDF가 된다는 참인 명제로 대우 격인 CDF를 미분하면 PDF가 된다. 이렇게 말해도 되나..

정규분포의 경우엔 확률 공간 중간의 CDF는 0.5를 나타낼 것이다. 

정규분포(normal distribution)

많은 통계적 분석에서는 오차가 정규분포를 따름을 가정하고 있다. 그리고 다양한 자연법칙 및 측정할 수 있는 대상들 (몸무게, 혈압, 키 등...)도 정규분포를 따른다고 한다.

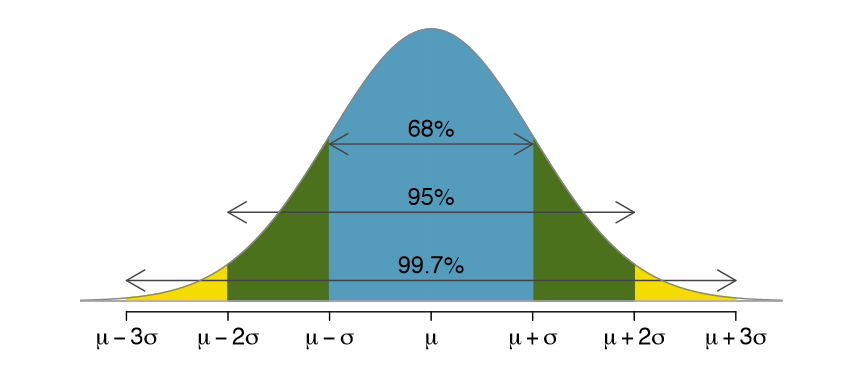
정규분포의 모양은 평균을 중심(line of symmetry)으로 좌우가 대칭이다. 데칼코마니를 생각나게 하는 모양으로 접힌 선을 중심으로 좌우에 50%씩 분포하고 있는 모양이다. 

중간으로 부터 양쪽 1시그마(표준편차)의 경우 68%, 2시그마는 95%... 

이걸 68-95-99.7 Rule이라고 부르기도 한다고 한다네